Фотограмметрия (от фото..., греч. grámma – запись, изображение и ...метрия) - научно-техническая дисциплина, занимающаяся определением размеров, формы и положения объектов по их изображениям на фотоснимках. Последние получают как непосредственно кадровыми, щелевыми и панорамными фотоаппаратами, так и при помощи радиолокационных, телевизионных, инфракрасных-тепловых и лазерных систем. Наибольшее применение, особенно в аэрофотосъёмке, имеют снимки, получаемые кадровыми фотоаппаратами. В теории фотограмметрии такие снимки считаются центральной проекцией объекта. Уклонения от центральной проекции, вызванные дисторсией объектива, деформацией фотоматериала и другими источниками ошибок, учитываются по данным калибровки аэрофотоаппарата и снимков. В фотограмметрии используются одиночные снимки и стереоскопические их пары. Эти стереопары позволяют получить стереомодель объекта. Раздел фотограмметрии, изучающий объекты по стереопарам, называется стереофотограмметрией.
Положение снимка в момент фотографирования определяют три элемента внутреннего ориентирования – фокусное расстояние фотокамеры f, координаты Xo, Yo главной точки о (рис. 1) и шесть элементов внешнего ориентирования – координаты центра проекции S – Xs, Ys, Zs, продольный и поперечный углы наклона снимка α и ω и угол поворота χ.
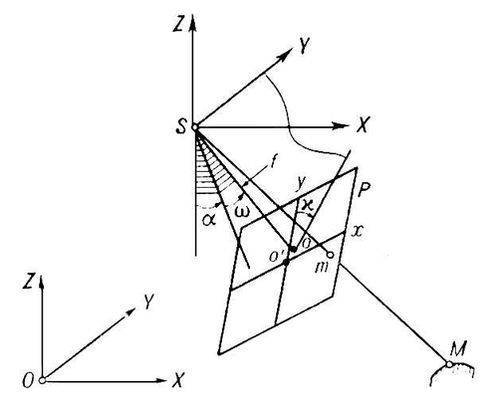
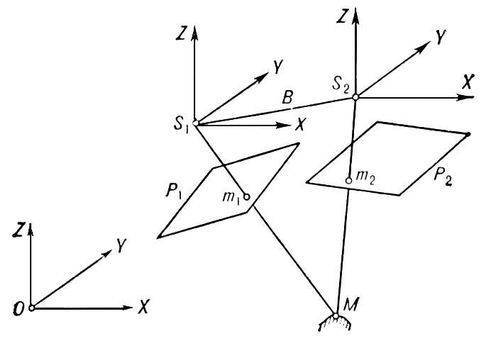
Между координатами точки объекта и её изображения на снимке существует связь (1):
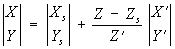
где X, Y, Z и Xs, Ys, Zs – координаты точек М и S в системе OXYZ; X’, Y’, Z’ – координаты точки m в системе SXYZ, параллельной OXYZ, вычисляемые по плоским координатам х и у (2):
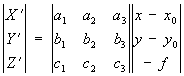
Здесь (3)
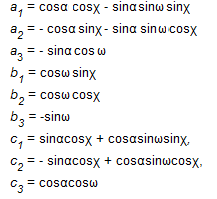
– направляющие косинусы.
Формулы связи между координатами точки М объекта (рис. 2) и координатами её изображений m1 и m2 на стереопаре P1 – P2 имеют вид (4):
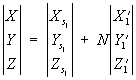
где (5)
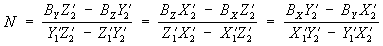
Bx, By и Bz – проекции базиса В на оси координат. Если элементы внешнего ориентирования стереопары известны, то координаты точки объекта можно определить по формуле (4) (метод прямой засечки). По одиночному снимку положение точки объекта можно найти в частном случае, когда объект плоский, например равнинная местность (Z = const). Координаты х и у точек снимков измеряются на монокомпараторе или стереокомпараторе. Элементы внутреннего ориентирования известны из результатов калибровки фотоаппарата, а элементы внешнего ориентирования можно определить при фотографировании объекта или в процессе фототриангуляции. Если элементы внешнего ориентирования снимков неизвестны, то координаты точки объекта находят с использованием опорных точек (метод обратной засечки).
Опорная точка – опознанная на снимке контурная точка объекта, координаты которой получены в результате геодезических измерений или из фототриангуляции.
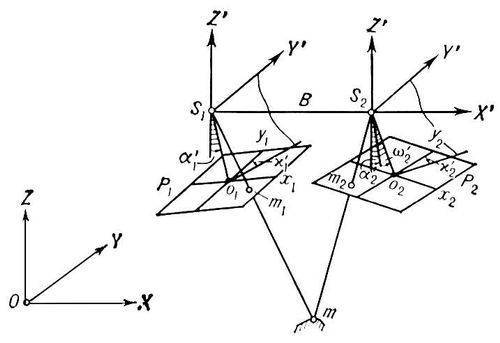
Применяя обратную засечку, сначала определяют элементы взаимного ориентирования снимков
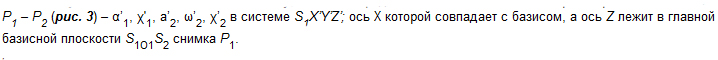
Затем вычисляют координаты точек модели в той же системе. Наконец, используя опорные точки, переходят от координат точек модели к координатам точек объекта.

Полагая, что приближённые значения элементов взаимного ориентирования известны, можно представить уравнение (6) в линейном виде:

Для определения элементов взаимного ориентирования измеряют координаты не менее пяти точек стереопары, а затем составляют уравнения (7) и решают их способом последовательных приближений. Координаты точек модели вычисляют по формулам (4), выбрав произвольно длину базиса В и полагая Xs1 = Ys1= Zs1=0, Bx = В, By = Bz = 0. При этом пространственные координаты точек m1 и m2 находят по формулам (2), а направляющие косинусы – по формулам (3):
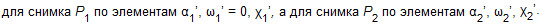
По координатам X’ Y’ Z’ точки модели определяют координаты точки объекта (8):
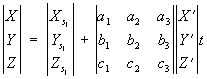
где t – знаменатель масштаба модели. Направляющие косинусы получают по формулам (3), подставляя вместо углов α, ω и χ продольный угол наклона модели ξ, поперечный угол наклона модели η и угол поворота модели θ.

уравнения (8) для трёх или более опорных точек и решают их. Координаты опорных точек находят геодезическими способами или методом фототриангуляции. Совокупность точек объекта, координаты которых известны, образует цифровую модель объекта, служащую для составления карты и решения различных инженерных задач, например для изыскания оптимальной трассы дороги. Кроме аналитических методов обработки снимков, применяются аналоговые, основанные на использовании фотограмметрических приборов – фототрансформатора, стереографа, стереопроектора и др.
Щелевые и панорамные фотоснимки, а также снимки, полученные с применением радиолокационных, телевизионных, инфракрасных-тепловых и других съёмочных систем, существенно расширяют возможности Ф., особенно при космических исследованиях. Но они не имеют единого центра проекции, и элементы внешнего ориентирования их непрерывно изменяются в процессе построения изображения, что осложняет использование таких снимков для измерительных целей.
Основные достоинства фотограмметрических методов работ:
Фотограмметрия широко применяется для создания карт Земли, других планет и Луны, измерения геологических элементов залегания пород и документации горных выработок, изучения движения ледников и динамики таяния снежного покрова, определения лесотаксационных характеристик, исследования эрозии почв и наблюдения за изменениями растительного покрова, изучения морских волнений и течений и выполнения подводных съёмок, изысканий, проектирования, возведения и эксплуатации инженерных сооружений, наблюдения за состоянием архитектурных ансамблей, зданий и памятников, определения в военном деле координат огневых позиций и целей и др.
Литература:
Бобир Н. Я., Лобанов А. Н., Федорук Г. Д., Фотограмметрия, М., 1974;
Дробышев Ф. В., Основы аэрофотосъемки и фотограмметрии, 3 изд., М., 1973;
Коншин М. Д., Аэрофотограмметрия, М., 1967;
Лобанов А. Н., Аэрофототопография, М., 1971;
Лобанов А. Н., Фототопография, 3 изд., М., 1968;
Дейнеко В. Ф., Аэрофотогеодезия, М., 1968;
Соколова Н. А., Технология крупномасштабных аэротопографических съемок, М., 1973;
Русинов М. М., Инженерная фотограмметрия, М., 1966;
Rüger W., Buchholtz A., Photogrammetrie, 3 Aufl, B., 1973;
Manual of photogrammetry, v. 1–2, Menasha, 1966;
Bonneval Н., Photogrammétrie générate, t. 1–4, P., 1972;
Piasecki М. B., Fotogrametria, 3 wyd., Warsz., 1973.
А. Н. Лобанов.








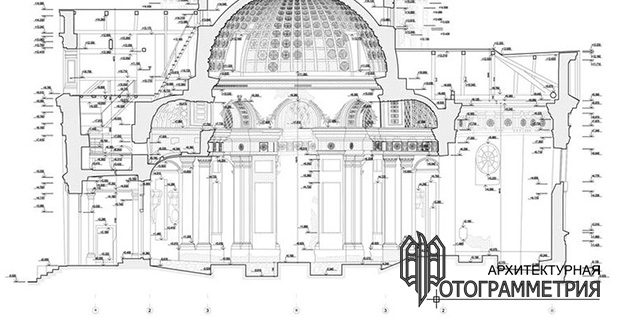

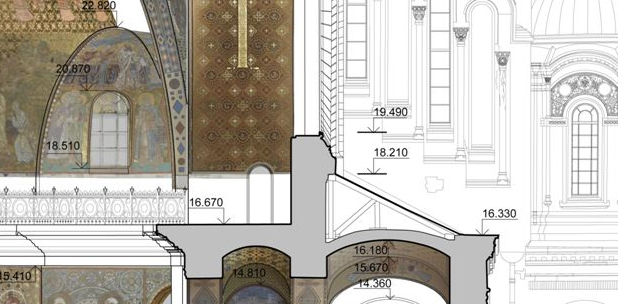



 Программный комплекс ScanIMAGER предназначен для обработки результатов трехмерного лазерного сканирования применительно к архитектурным обмерам. Он построен по модульному принципу и поставляется в различных модификациях.
Программный комплекс ScanIMAGER предназначен для обработки результатов трехмерного лазерного сканирования применительно к архитектурным обмерам. Он построен по модульному принципу и поставляется в различных модификациях.