Несмотря на то, что общая форма и размеры Земли изучаются уже много веков, до настоящего времени о них нет таких данных, которые дали бы возможность составить уравнение ее поверхности и вполне соответствовали бы современной точности измерений.
Физическая поверхность Земли имеет сложную форму: 71 % ее поверхностной площади занимают моря и океаны и только 29 % — суша. Однако самые высокие горы и самые большие глубины океанов, по сравнению с размерами всей Земли, ничтожно малы. Например, на глобусе диаметром в 60 см вершина Джомолунгма (Эверест), высотой 8848 м, будет изображена всего лишь как крупинка диаметром 0,25 мм. Средняя глубина Мирового океана 3794 м и средняя высота суши над уровнем океана — 875 м.
В истории изучения фигуры Земли можно выделить следующие основные периоды:
1) с древнейших времен до конца XVI в., когда Землю считали шаром;
2) с конца XVI в. до второй половины XIX в., когда ее считали несколько сплюснутым у полюсов шаром, сфероидом;
3) со второй половины XIX в. до 40-х гг. XX в., когда было установлено, что эллипсоид вращения — сфероид — является только вторым приближением к истинной форме Земли (считая за первое шар). И что будет правильно представлять ее трехосным эллипсоидом, хотя трехосный эллипсоид является приближенным отображением более сложной формы земного шара, названной геоидом;
4) с 40-х гг. XX в. по настоящее время, когда за фигуру Земли принимают сложное тело, ограниченное физической поверхностью Земли.
Геодезические измерения, выполняемые в любой точке физической поверхности, связаны с направлением отвесной линии в этой точке. Например, при измерении горизонтального угла теодолит устанавливают по уровню в вершине измеряемого угла так, чтобы вертикальная ось инструмента была совмещена с отвесной линией в данной точке.
Простейший прибор — отвес — показывает направление действия силы тяжести; подвешенный на нити груз под действием силы тяжести натягивает нить, которая и указывает направление отвесной линии в данной точке.
Известно, что сила тяжести G есть равнодействующая двух сил: силы притяжения F и силы тяготения Р (рис. 2).
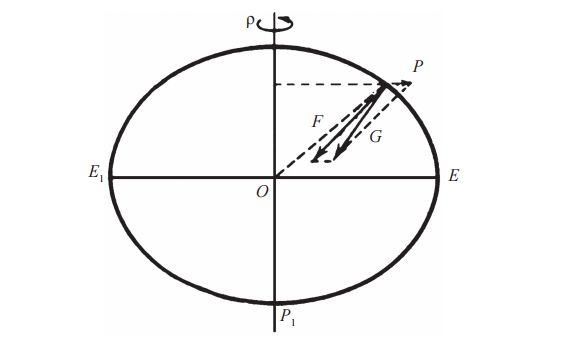
Рис. 2. К понятию о силе тяжести
Вектор силы тяготения F направлен приблизительно к центру Земли. Наибольшее значение сила F имеет на полюсах и наименьшее на экваторе. Центробежная сила Р максимальное значение имеет на экваторе, где она составляет приблизительно 1/288 от величины силы F. На полюсах сила Р равна нулю. Следовательно, сила тяжести на земной поверхности непрерывно увеличивается от экватора к полюсам, и на полюсах имеет максимальное значение.
В свою очередь, сила земного притяжения F есть равнодействующая притяжения всех масс, заключенных в теле Земли. Значит, величина и направление силы обусловлены распределением этих масс. Отсюда следует, что и направление отвесной линии тоже зависит от распределения масс в теле Земли.
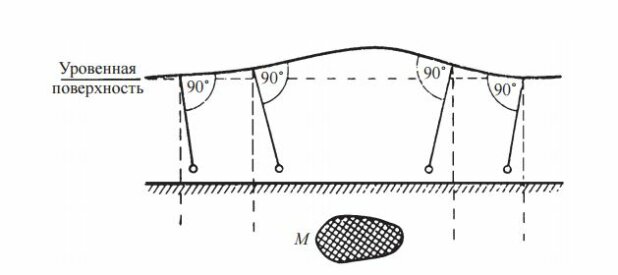
При равномерном распределении масс уровенная поверхность будет занимать положение, указанное пунктиром. При наличии массы М с преувеличенной плотностью уровенная поверхность будет иметь некоторый выгиб кверху (рис. 3).
Также известно, что в гравитационном поле Земли работа силы тяжести не зависит от формы пути, а зависит только от положения начальной и конечной точек этого пути.
Поле, обладающее таким свойством, называется потенциальным. Во всяком потенциальном поле можно провести так называемые поверхности уровня, т. е. такие поверхности, при движении материальной точки по которым сила поля работы не совершает.
Вид уровенной поверхности зависит от распределения масс в теле Земли. Линии, нормальные к уровенным поверхностям, называются силовыми линиями.
Касательная к силовой линии в данной точке есть отвесная линия в этой точке. Следовательно, отвесная линия является нормалью к уровенной поверхности (рис. 4).
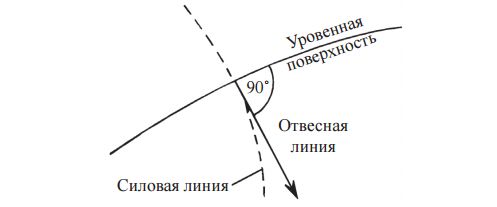
Рис. 4. Направление отвесной линии
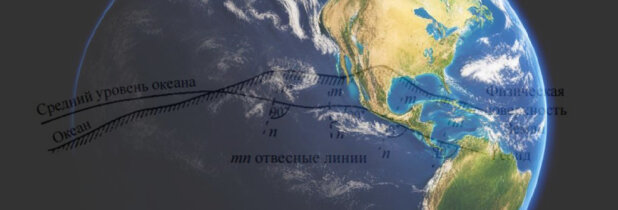
Поверхность воды в спокойном состоянии будет одной из уровенных поверхностей. Геодезические измерения связаны с направлением отвесной линии в тех точках, в которых они выполнялись.
Значит, в каждой такой точке результаты измерений могут быть отнесены именно к той уровенной поверхности, которая проходит через данную точку. Но в таком случае результаты измерений на пунктах какой-либо геодезической сети окажутся отнесенными к различным уровенным плоскостям и замкнутых фигур в сети не образуют. В связи с этим возникает необходимость приведения результатов всех геодезических измерений прежде всего к некоторой данной или принятой в качестве общей исходной уровенной поверхности. Практически в качестве основной уровенной поверхности берут так называемый средний уровень океана (моря), определяемый из многолетних наблюдений уровня моря по футштокам на морских водомерных станциях. В России основным является Кронштадтский футшток, по которому уровень Балтийского моря наблюдался с 1825 г. Нуль Кронштадтского футштока соответствует среднему уровню Балтийского моря и принят за начало счета
абсолютных высот для всех геодезических сетей.
Геоид. Если основную уровенную поверхность мысленно продолжить под континентами так, чтобы в любой ее точке отвесная линия была перпендикулярна к этой поверхности, то будет образована сплошная замкнутая поверхность без складок, охватывающая почти всю массу Земли.
Геометрическое тело, ограниченное основной уровенной поверхностью, по предложению в 1873 г. немецкого физика Листинга (1808–1882) принято называть геоидом.
Итак, геоидом называется геометрическое тело, поверхность которого совпадает с невозмущенной поверхностью океана и мысленно продолжена под континентами так, что в каждой точке этой поверхности отвесная линия перпендикулярна к ней.
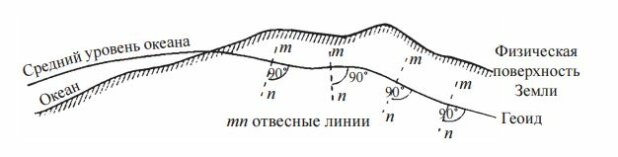
Геоид хорошо представляет Землю в целом, и потому до недавнего времени в геодезии под фигурой Земли понималась именно поверхность геоида. Изучение этой поверхности считалось основной научной задачей в геодезии. Однако вследствие неравномерного распределения масс в теле Земли поверхность геоида, как одна из уровенных поверхностей поля силы тяжести Земли, имеет сложный волнистый вид (рис. 5).
Различают большие и малые волны геоида. Большие волны обусловлены значительными неравномерностями распределения масс, они соответствуют океанам и континентам. Малые волны — результат влияния местных условий, например, отдельных горных хребтов. Волны геоида имеют высоты порядка нескольких метров и десятков метров, однако не превышают 100–150 м.
Изучение формы геоида встречает принципиальные затруднения. Это обусловлено тем, что для определения поверхности геоида относительно поверхности сравнения (допустим, относительно поверхности эллипсоида) необходимо знать кривизну силовых линий гравитационного поля в пространстве между физической поверхностью Земли и поверхностью геоида. Но кривизна силовых линий зависит от распределения масс в теле Земли, а поскольку это распределение остается неизвестным, строгое решение задачи определения фигуры геоида остается невозможным.
Из обработки градусных и спутниковых измерений установлено, что поверхность геоида является довольно сложной из-за неоднородностей гравитационного поля Земли. Наибольшие отрицательные высоты геоида наблюдаются в районе Индийского океана (около –105 м) и вблизи Антарктиды (в море Росса до –61 м), а наибольшие положительные высоты — в Тихом океане (около Новой Гвинеи до +77 м) и в Северной Атлантике (до +66 м). Фигура Земли в целом имеет грушеобразную форму (апиоид): северное полушарие возвышается над полюсом на 20–30 м, а южное, наоборот, вдавлено на ту же величину [1, с. 23].
На основании ряда исследований М. С. Молоденский пришел к выводу, что основной научной проблемой геодезии следует считать не определение фигуры геоида, как это понималось раньше, а изучение внешнего гравитационного поля и фигуры физической поверхности Земли, поскольку фигура геоида зависит от неизвестного нам распределения масс, то она, строго говоря, неопределима.
Квазигеоид. Для изучения формы физической поверхности Земли М. С. Молоденский предложил некоторую вспомогательную поверхность, весьма близкую к поверхности геоида и названную им квазигеоидом. Эта вспомогательная поверхность, или квазигеоид, определяется по результатам только одних астрономо-геодезических и гравиметрических измерений на физической поверхности Земли без приведения их к какой-нибудь другой поверхности.
На океанах и морях поверхности геоида и квазигеоида совпадают, на континентах — расходятся: в равнинных районах на несколько сантиметров, в горных и высокогорных около 1–2 м.
Общий земной эллипсоид. Решение геодезических задач (решение треугольников, вычисление координат, азимутов и т. д.) непосредственно на физической поверхности Земли невозможно вследствие неправильности этой поверхности.
Геоид в целом весьма близко подходит к эллипсоиду вращения с малым сжатием — фигуре, хорошо изученной в математическом
отношении.
Эллипсоид, лучше всего подходящий к фигуре геоида в целом, называется общим земным эллипсоидом (рис. 6). Определение параметров этого эллипсоида является одной из основных задач высшей геодезии и подчиняется следующим условиям:
1. Центр эллипсоида должен совпадать с центром инерции Земли, а малая ось — с осью вращения Земли.
2. Объем эллипсоида должен быть равен объему геоида.
3. Сумма квадратов отклонений по высоте поверхности геоида и по высоте поверхности эллипсоида должна быть наименьшей.
4. Масса всей Земли должна равняться массе эллипсоида — это связано с определением гравитационного поля. В настоящее время масса Земли составляет 6 • 1027 г, Солнца — 2 • 1033 (что примерно в 333 000 раз больше, чем масса Земли). Масса Земли вызывает на экваторе ускорение 978,038 см/с2. Плотность пород Земли составляет в среднем 5,5 г/см3, плотность горных пород на поверхности — 2,75 г/см3, в ядре — 13 г/см3, что соответствует жидкому железу.
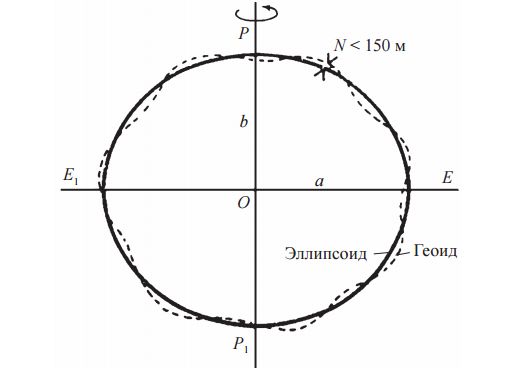
Рис. 6. Общий земной эллипсоид
Общий земной эллипсоид не определен из-за недостаточности астрономо-геодезических измерений и из-за того, что не вся Земля покрыта гравиметрической сетью.
В нашей стране до 1946 г. пользовались эллипсоидом, размеры которого были получены Ф. Бесселем (1784–1846).
В 1940 г. Ф. Н. Красовским (1878–1948) при участии профессора А. А. Изотова были определены размеры эллипсоида вращения (a = 6 378 245 м, b = 6 356 863 м, α = 1 : 298,3), наиболее подходящие для нашей территории. Постановлением Совета министров СССР № 760 от 7 апреля 1946 г. эллипсоид указанных размеров был принят для производства всех видов геодезических и картографических работ в нашей стране и назван эллипсоидом Красовского [12, с. 8].
Референц-эллипсоид. Для использования того или иного эллипсоида (из числа известных) при решении геодезических задач нужно знать не только его размеры, но и положение в теле Земли, т. е. эллипсоид должен быть определенным образом ориентирован в теле Земли. Такой эллипсоид называется референц-эллипсоидом — «рабочим эллипсоидом», который выведен по результатам геодезических работ, охватывающих территорию данной страны или ее части, или нескольких стран.
В разное время многие ученые по имеющимся в их распоряжении материалам определяли размеры земного эллипсоида. Некоторые из важнейших определений приведены в табл. 1.
| Название эллипсоида | Большая полуось, а (м) | Сжатие, α |
| Эллипсоид Даламбера (1800) | 6 375 653 | 1 : 334,0 |
| Эллипсоид Бесселя (1841) | 6 377 397 | 1 : 299,2 |
| Эллипсоид Хейфорда (1910) | 6 378 388 | 1 : 297,0 |
| Эллипсоид Красовского (1940) | 6 378 245 | 1 : 298,3 |
Итак, референц-эллипсоидом называется эллипсоид вращения с определенными размерами его полуосей, определенным образом ориентированный в теле Земли и принятый для геодезических работ в данной стране.
Референц-эллипсоиды отличаются от общего земного эллипсоида. Это различие заключается в несовпадении размеров и центров референц-эллипсоидов с размерами и центрами общего земного эллипсоида, а условие минимума суммы квадратов отклонений выполняется для референц-эллипсоида не для всей поверхности Земли, а только для той части, на которой были выполнены геодезические работы, результаты которых использованы для вывода его параметров.
Такие эллипсоиды служат координатной поверхностью, на которой решаются геодезические задачи и относительно которой определяются геодезические координаты пунктов. Геодезические координаты определяют направление нормалей к поверхности эллипсоида.
Эллипсоид — это идеализируемая земная поверхность. Такая идеализация нужна для решения целого ряда практических задач:
определения координат различных точек на поверхности Земли, вычисления расстояний между удаленными точками и т. п.
Эллипсоид — это поверхность аналитическая, точно выражаемая математическими формулами. Нет такой правильной геометрической фигуры, которой можно было бы точно описать Землю, которая в первом приближении похожа на шар. Еще точнее — на эллипсоид. Наконец, был придуман геоид.
Такой геометрической поверхности, как геоид, нет, но есть физическое понятие уровенной поверхности. Изучив силы тяготения, можно определить эту поверхность. Но Земля не жидкая и не однородная, большая ее часть покрыта слоем воды (моря и океаны) и значительная ее часть все же твердая (континенты и острова).
Их нельзя представить ни эллипсоидом, ни геоидом, ни какой-либо другой правильной поверхностью. Континенты и острова все равно «вылезают» за нее. Нам надо знать именно эту реальную поверхность Земли, на которой мы живем и которая существует в природе, но нет, однако, ее физико-математического (геометрического) эквивалента.
На сегодняшний день, чтобы представить фигуру Земли с любой необходимой нам точностью, следует знать:
• большую полуось и сжатие эллипсоида относимости;
• элементы ориентирования этого эллипсоида в теле Земли, т. е. высоту, широту, долготу исходного пункта и азимут направления, например, большой полуоси (высота геоида в пространстве над референц-эллипсоидом равна нулю). Геодезическая широта круглого зала Пулковской обсерватории B = 59°46', равная астрономической широте φ; геодезическая долгота L = 30°19'28'', равная астрономической долготе λ и геодезический азимут А, равный астрономическому азимуту α. От этих координат идет вычисление координат пунктов на всей территории страны.
• множество высот физической поверхности Земли над геоидом, или, что то же самое, над уровнем моря;
• множество высот геоида над эллипсоидом относимости.
Нормальная Земля. При решении геодезических задач в масштабе всей Земли за поверхность относимости целесообразно принять поверхность общего земного эллипсоида (нормальная Земля).
Некоторые параметры нормальной Земли получили название фундаментальных геодезических постоянных. К ним в настоящее время относятся следующие величины: f • M — произведение универсальной гравитационной постоянной на массу уровенного эллипсоида, а — большая полуось, I2 — нормальный гармонический коэффициент геопотенциала второй степени, ω — угловая скорость вращения Земли.
Фундаментальные геодезические постоянные определяют, используя результаты наблюдений ИСЗ, далеких космических летательных аппаратов (КЛА), а также результаты астрометрических и гравиметрических измерений.
В 1979 г. в Канберре в соответствии с рекомендацией XVII Генеральной ассамблеи Международного геодезического и геофизического союза приняты следующие значения фундаментальных геодезических постоянных:
f • M = (3 896 005 ± 0, ) • 108 м3;
I2 = (108 263 ± 0,5) • 10–8 ;
а = 6 378 137 ± 2 м;
ω = 7 292 115 • 10–11рад • с–1;
α = 1 : 298,257 ± 0,001 — полярное сжатие Земли;
γе = 978 033 ± 1 мГал — нормальная сила тяжести γе на экваторе уровенного эллипсоида.
Астрономо-геодезическим уклонением отвесной линии называется угол u между нормалью к поверхности эллипсоида и отвесной линией в данной точке. Различают абсолютное и относительное уклонение отвесных линий.
Под абсолютным уклонением отвесной линии в точке М понимают угол u1 между нормалью Мn1 к общему земному эллипсоиду и направлением отвесной линии Мg в данной точке М (рис. 7).
Относительным уклонением отвесной линии в точке М называется угол u2 между нормалью Мn2 к поверхности референц-эллипсоида и отвесной линией Мg в данной точке M, по величине относительные уклонения больше абсолютных. Наибольшие отклонения поверхности геоида (квазигеоида) от поверхности общего земного эллипсоида не превышают 120 м, т. е. они сравнительно малы, поэтому сравнительно малы и абсолютные уклонения отвесных линий. В равнинной местности уклонения отвесных линий составляют в среднем от 3" до 5", иногда достигают 10"–15", в горных районах, в районе озера Байкал ~30".
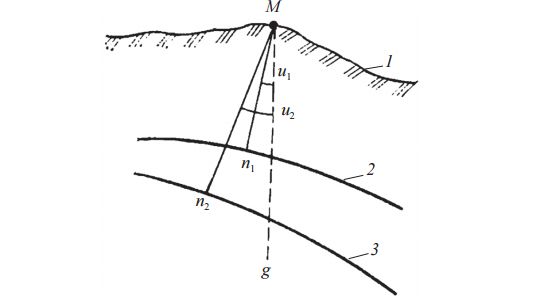
Рис. 7. Абсолютное и относительное уклонения отвесных линий:
1 — физическая поверхность Земли; 2 — общий земной эллипсоид;
3 — референц-эллипсоид
Самые большие уклонения отвесных линий на земном шаре обнаружены в районе Гавайских островов (97").
Основы геодезии: учеб. пособие / Т. И. Левитская; М-во образования и науки Рос. Федерации, Урал. федер. ун-т. —
2-е изд., перераб. — Екатеринбург: Изд-во Урал. ун-та, 2017.
В учебном пособии изложены общие сведения по геодезии. Показана связь геодезии с другими науками. Приведены исторические сведения о фигуре и размерах Земли. Изложена сущность картографических проекций. Особое внимание уделено ориентированию направлений на местности и на карте. Дано определение ориентирующих углов и связи между ними. Изложены вопросы определения положений точек местности на земной поверхности.
Учебное пособие предназначено для студентов бакалавриата первого курса, обучающихся по направлению подготовки «Геодезия и дистанционное зондирование», может быть рекомендовано также студентам-историкам и археологам, интересующимся вопросами геодезии.
#геодезия #формаЗемли #геоид #геодезическиеИзмерения #обмерныеработы












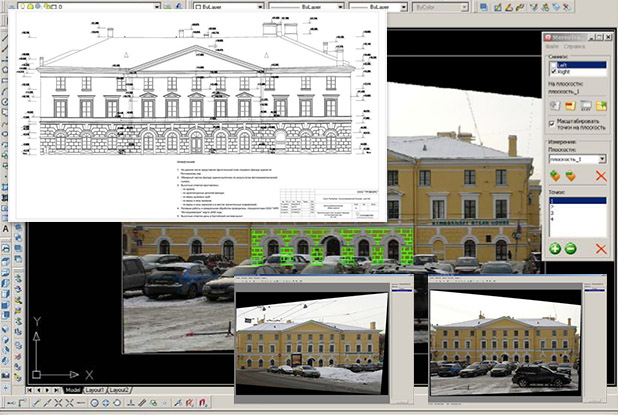



 Программный комплекс ScanIMAGER предназначен для обработки результатов трехмерного лазерного сканирования применительно к архитектурным обмерам. Он построен по модульному принципу и поставляется в различных модификациях.
Программный комплекс ScanIMAGER предназначен для обработки результатов трехмерного лазерного сканирования применительно к архитектурным обмерам. Он построен по модульному принципу и поставляется в различных модификациях.