В геодезии часто приходится передавать координаты с одной точки (пункта) на другую.
Зная исходные координаты данной точки, горизонтальное расстояние до другой точки и направление линии, соединяющей их (азимут, дирекционный угол или румб), можно определить координаты второй точки (пункта) — в этом заключается решение прямой геодезической задачи.
Данная задача представляет значительные трудности при ее решении для точек, расположенных на эллипсоиде. Для точек на плоскости она решается следующим образом.
Пусть AB — одна из сторон полигона (теодолитного хода), для которой известна горизонтальная проекция d и дирекционный угол α (рис. 29). Координаты точки A (x1, y1) также известны.
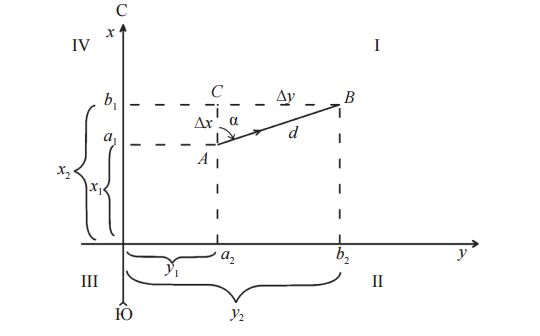
Рис. 29.Прямая геодезическая задача
Требуется найти координаты второй точки B (x2, y2). Из рис. 29 имеем:
x2 – x1 = Δx,
y2 – y1 = Δy. (38)
Разности Δx и Δy координат последующей и предыдущей точек называются приращениями координат.
Из прямоугольного треугольника ABC имеем:
Δx = d cos α,
Δy = d sin α. (39)
Так как d — всегда число положительное, то знаки приращений координат Δx и Δy зависят от знака cos α, sin α.
Для различных значений углов α знаки Δx и Δy могут быть представлены так, как показано в табл. 3 или на рис. 30.
Определение румбов сторон хода и знаки приращений координат
| Приращение | Четверть окружности, к которой относится α | |||
| I, или СВ | II, или ЮВ | III, или ЮЗ | IV, или С | |
| Δx | + | - | - | + |
| Δy | + | + | - | - |
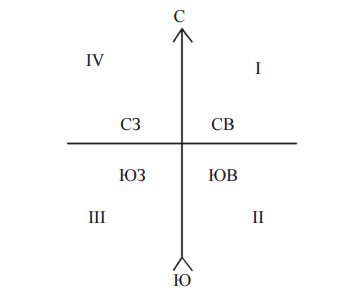
Рис. 30. Нумерация четвертей и их названия
При помощи румба приращения координат вычисляем по формулам
Δx = d cos r,
Δy = d sin r.(40)
Знаки приращениям дают в зависимости от названия румба.
Вычислив приращения координат, искомые координаты точки B (или другой точки) можно найти по формулам
x2 = x1 + Δx,
y2 = y1 + Δy.(41)
Этим способом можно найти координаты любого числа точек по правилу, вытекающему из формулы (41): координата последующей точки равна координате предыдущей точки плюс соответствующее приращение.
Обратная геодезическая задача состоит в том, чтобы по данным координатам точек A и B найти длину и направление (дирекционный угол, румб) отрезка AB.
Имея координаты точек A(x1, y1), B(x2, y2), находим по формулам (38) приращения координат. Из формулы (39) имеем: d = Δx/cos α = = Δy/sin α. Тогда, учитывая формулы (39) и (40), получим:
tg α = Δy/ Δx, (42)
tg r = Δy/ Δx, (43)
d = (Δx2 + Δy2 )1/2. (44)
По формуле (42) находят величину угла α, а по знакам приращений определяют четверть, в которой он располагается, и название румба, вычисленного по формуле (43).
Найдя α и r, вычисляют дважды (для контроля) расстояние d при помощи формул (39) или (44).
Основы геодезии: учеб. пособие / Т. И. Левитская; М-во образования и науки Рос. Федерации, Урал. федер. ун-т. —
2-е изд., перераб. — Екатеринбург: Изд-во Урал. ун-та, 2017.
В учебном пособии изложены общие сведения по геодезии. Показана связь геодезии с другими науками. Приведены исторические сведения о фигуре и размерах Земли. Изложена сущность картографических проекций. Особое внимание уделено ориентированию направлений на местности и на карте. Дано определение ориентирующих углов и связи между ними. Изложены вопросы определения положений точек местности на земной поверхности.
Учебное пособие предназначено для студентов бакалавриата первого курса, обучающихся по направлению подготовки «Геодезия и дистанционное зондирование», может быть рекомендовано также студентам-историкам и археологам, интересующимся вопросами геодезии.
#геодезия #прямаяГеодезическаяЗадача #обратнаяГеодезическаяЗадача #координатыТочек #учебноепособие














 Программный комплекс ScanIMAGER предназначен для обработки результатов трехмерного лазерного сканирования применительно к архитектурным обмерам. Он построен по модульному принципу и поставляется в различных модификациях.
Программный комплекс ScanIMAGER предназначен для обработки результатов трехмерного лазерного сканирования применительно к архитектурным обмерам. Он построен по модульному принципу и поставляется в различных модификациях.