Основные случаи наземной стереофотограмметрической съемки
Существует несколько вариантов выполнения наземной стереофотограмметрической съемки. Они зависят от формы и размера объекта съемки, а также от его местоположения относительно точек фотосъемки.
Общий случай фотосъемки
В отличие от аэрофотосъемки, углы наклона наземных снимков могут принимать произвольные значения (от 0o до 360o).
На рис. 1 показан пример возможной съемки для получения модели пространственного объекта.
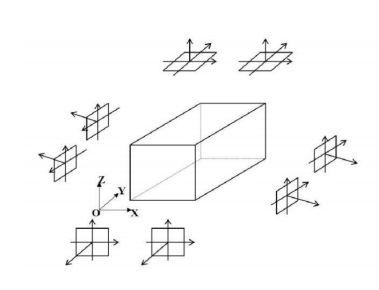
Рис. 1. Схема общего случая фотосъемки
НОРМАЛЬНЫЙ СЛУЧАЙ ФОТОСЪЕМКИ
В этом случае оптические оси фотокамер параллельны между собой и перпендикулярны базису фотографирования рис. 2.
При этом их взаимное угловое положение и относительно базиса имеют следующие значения:
α1 ≈ α2 ≈ 0o
ω1 ≈ ω2 ≈ 90o
κ1 ≈ κ2 ≈ 0o
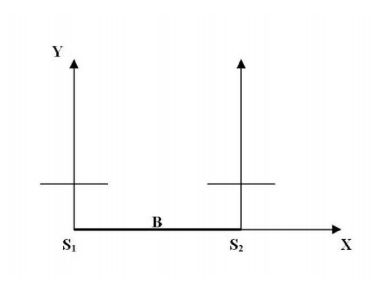
Рис. 2 Схема нормального случая фотосъемки
РАВНООТКЛОНЕННЫЙ СЛУЧАЙ ФОТОСЪЕМКИ
Оптические оси фотокамер параллельны между собой и отклонены от перпендикуляра к базису на некоторый угол рис. 3. Угловые элементы снимков имеют следующие значения:
α1 ≈ α2 ≈ α
ω1 ≈ ω2 ≈ 0o
κ1 ≈ κ2 ≈ 0o
Этот случай съемки используется для увеличения площади съемки с одного базиса фотографирования. Как правило, с одного базиса получают три стереопары: с отклонением влево, нормальный случай и с отклонением вправо.
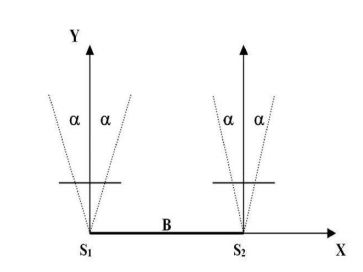
Рис. 3. Схема равноотклоненного случая фотосъемки
РАВНОНАКЛОННЫЙ СЛУЧАЙ ФОТОСЪЕМКИ
Оптические оси камер параллельны между собой и наклонены относительно горизонтальной плоскости на некоторый угол ω (рис.4). Угловые элементы снимков имеют следующие значения:
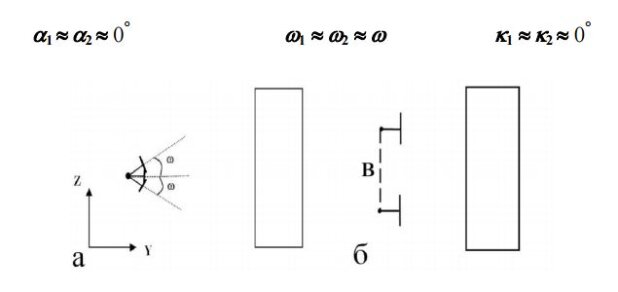
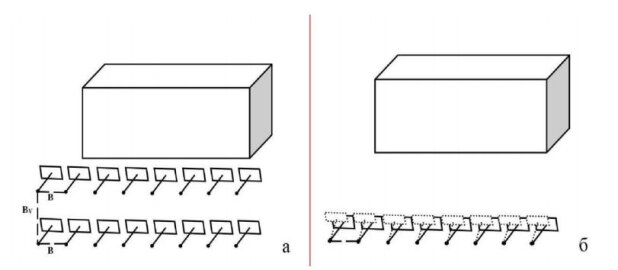
Рис. 4. Схема фотосъемки высоких сооружений: а- равнонаклонный случай фотосъемки, б – фотосъемка с вертикального базиса
Этот случай фотосъемки применяется, когда надо снять высокий объект (например, многоэтажное здание).
В ряде случаев, при фотосъемке высоких сооружений, целесообразно производить получение стереопар снимков нормального, равноотклоненного и равнонаклонного случаев фотосъемки с вертикального базиса (рис. 4б).
КОНВЕРГЕНТНЫЙ СЛУЧАЙ ФОТОСЪЕМКИ
Оптические оси фотокамер не параллельны между собой, а повернуты навстречу друг другу под углом γ, который называется углом конвергентности (рис. 5). Это позволяет повысить точность определения координат точек объекта за счет увеличения длины базиса фотографирования.
Однако с увеличением угла конвергенции, а также, если объект имеет выступы, может потеряться его стереоскопическое восприятие, как в целом, так и его отдельных частей. Данный случай фотосъемки можно применить, например, для получения координат маркированных на объекте точек с более высокой точностью, т.к. на них на обоих снимках марки можно навести монокулярно.
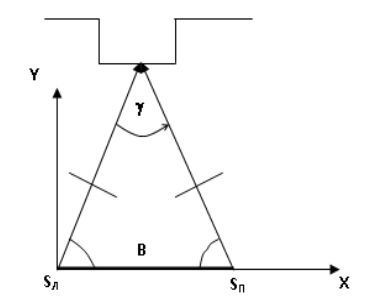
Рис. 5. Конвергентный случай фотосъемки
Маршрутная и блочная фотосъемки
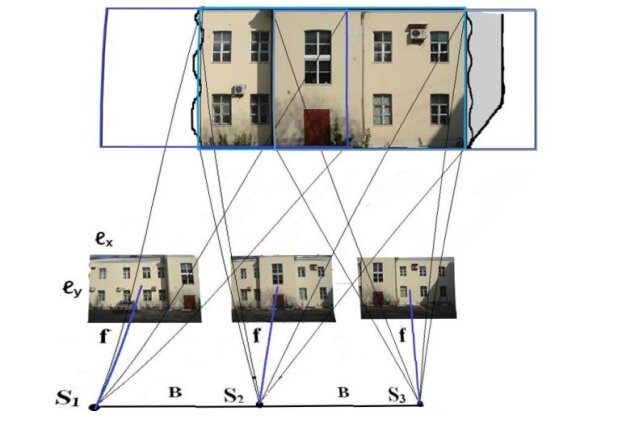
При съемке протяженных объектов целесообразно производить маршрутную или блочную фотосъемку объекта. В качестве примера на рис. 6 представлен вариант маршрутной фотосъемки здания.
В маршрутной фотосъемке из смежных снимков маршрута, формируется стереопары снимков нормального или равнонаклонного случаев съемки. При этом фотосъемка выполняется таким образом, чтобы у смежных стереопар имелась область так называемого тройного перекрытия. Для этого фотосъемку выполняют таким образом, чтобы смежные снимки в маршруте перекрывались по направлению маршрута приблизительно на 60%.
В случае если при проведении маршрутной фотосъемки объект изображается на снимках по высоте не полностью, производят блочную (многомаршрутную) фотосъемку, в которой выполняют дополнительную маршрутную фотосъемку объекта, формируя один или несколько параллельных маршрутов с поперечным перекрытием маршрутов не меньше 20–30%.
Возможны два варианта проведения блочной съемки (рис.7). В первом варианте маршрутные съемки производят с разных высот, например, с поверхности земли и крыши здания (рис. 7а).
Во втором варианте с каждой точки фотографирования получают снимки при разных углах наклона ω, из которых формируют перекрывающиеся маршруты из стереопар снимков нормального и равнонаклонного случаев съемки (рис. 7б).
На рис. 8 представлен пример блочной фотосъемки 16-ти этажного дома. Фасад снимался с двух отстояний. Расположение снимков, которые получились при фотосъемке, выделены синим цветом.
При выполнении наземной стереофотограмметрической съемки могут возникнуть так называемые «мертвые зоны» (участки объекта, не изобразившиеся на стереопаре снимков). Для съемки этих участков объекта производят фотосъемку с дополнительных базисов.

Рис. 8. Съемка высотного здания с двух отстояний
На рис. 9 мертвые зоны, возникающие при проведении съемки с точек фотографирования S1, S2, S3 показаны серым цветом. Съемки этих частей объекта необходимо выполнить с дополнительных станций (S4 – S5).
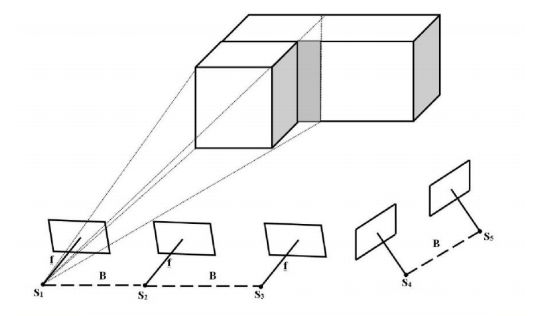
Рис. 9. Схема проектирования дополнительных маршрутов
Расчет оптимальных параметров фотосъемки
При выборе схемы съемки в любом случае приходится решать три основные задачи:
1. Обеспечить заданную точность определения координат точек объекта при минимальном количестве станций съемки. Для этого следует правильно выбрать отстояние камеры от объекта и величину базиса фотографирования.
2. Покрыть снимками весь изучаемый объект, чтобы отсутствовали мертвые зоны (части объекта, не зобразившиеся на снимках).
3. Обеспечить дешифрируемость объектов по снимкам (возможность опознавания на снимках мелких деталей объекта).
Рассмотрим более подробно каждую из этих задач.
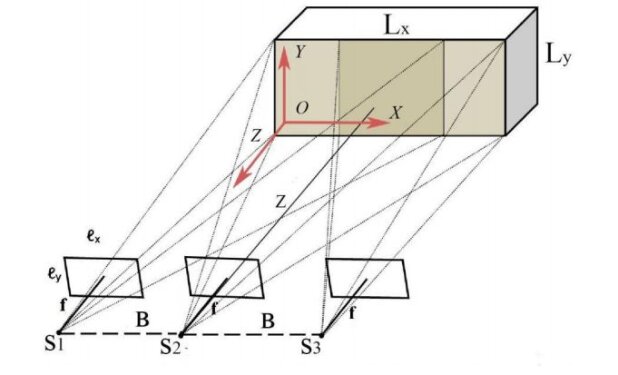
Наиболее часто для обмерных целей используется локальная система координат фасада, в которой ось X направлена вдоль фасада, ось Y перпендикулярна ей и направлена вверх, ось Z дополняет систему до правой (рис. 10).
Для обеспечения заданной точности определения координат точек объекта (mX, mY, mZ), необходимо рассчитать базис фотографирования B и максимальное отстояние камеры от объекта Z.
Эти вычисления можно выполнить в следующей последовательности:
Сначала вычисляют базис фотографирования b в масштабе снимка, задаваясь продольным перекрытием Px между снимками:
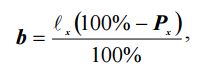
где ℓx – формат снимка вдоль оси x.
Затем нужно вычислить максимальное отстояние Z, при котором будет обеспечена заданная точность mZ определения координаты Z (вдоль оптической оси камеры) точек объекта (рис. 9), используя известную формулу:
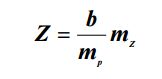 (2.4)
(2.4)где mp – средняя квадратическая погрешность измерения продольных параллаксов по снимкам.
Соответствующее значение базиса фотографирования на местности вычисляется по формуле:
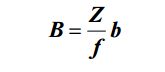 (2.5)
(2.5)Количество станций фотографирования определяется количеством базисов фотографирования необходимым для съемки объекта длиной L:
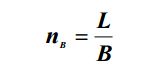 (2.6)
(2.6)Если при выполнении съемки придерживаться значений отстояния и базиса фотографирования, вычисленных по формулам (2.4–2.6), то при фотограмметрической обработке таких снимков точность определения координаты Z не будет ниже заданной mZ. Точность определения координат точек объекта mX, mY будет заведомо выше, чем mZ.
Рассмотрим конкретный пример вычисления оптимальных параметров съемки.
Предположим, что необходимо выполнить фотосъемку фасада здания (рис. 10) со следующими размерами: длина L = 25 м, высота H = 10 м. Цель – получение трехмерной модели этого фасада в локальной системе координат объекта OXYZ. Точность определения координат точек модели должна быть не хуже 1 см, т.е., mX, = mY = mZ = 0,01 м. Фотосъемку предполагается выполнять цифровой камерой Kodak DCS Pro14 с размером матрицы (формат снимка) 4500x3000 pix и фокусным расстоянием f = 4500 pix . Обработку снимков будет выполняться на цифровой фотограмметрической системе, обеспечивающей точность измерения продольных параллаксов порядка 0,5 пикселя, т.е. mp = 0,5 pix.
Продольное перекрытие Px возьмем равным 60%, обеспечивающее тройное перекрытие снимков с целью возможности построения фототриангуляции.
Тогда значение базиса фотографирования в масштабе снимка, согласно (2.4) будет следующее:
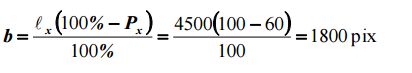
а максимальное отстояние фотокамеры от объекта будет:
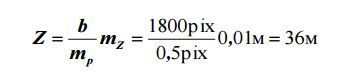
Базис фотографирования на местности в этом случае равен:
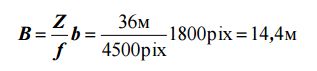
Таким образом, если выбрать длину базиса фотографирования не менее 14,4 м, а отстояние не более 36 м, то точность определения координат точек объекта по снимкам не будет превышать 1 см.
Зная длину объекта Lx, получим количество базисов фотографирования и число станций:
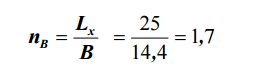
Если число базисов фотографирования получается дробным, то естественно его следует округлить, причем всегда в большую сторону, с тем чтобы покрыть фотосъемкой весь объект. В данном случае nB = 2. Двух базисов фотографирования или трех снимков достаточно для съемки всего объекта по его длине, как это показано на рис. 10.
Осталось выяснить изобразится ли весь объект по высоте на этих снимках. Это можно сделать, вычислив высоту захвата H данной фотокамерой для отстояния Z:
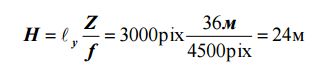
Здесь ℓy – формат кадра вдоль оси y. В нашем случае весь объект по высоте (10 м) будет изображен на этих снимках (рис. 10), т.е. всего достаточно трех снимков для решения поставленной задачи.
Предположим, что по условиям реальной местности подходы к данному объекту ограничены и нет возможности отойти от данного фасада здания на расстояние 36 м, например, ширина улицы всего 10 м, т.е. есть возможность установить камеру на максимальном отстоянии, равном 10 м. В этом случае, величина базиса фотографирования будет:
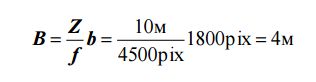
а количество базисов фотографирования:
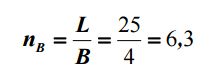
т.е. nB = 7 или 8 снимков в маршруте (рис. 7).
При этом захват кадра по высоте при 10 м отстояния будет:
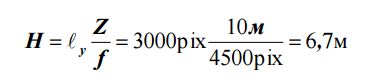
т.е. необходима дополнительная фотосъемка в виде второго маршрута, покрывающего верхнюю часть здания.
В таких случаях могут быть три варианта.
Первый вариант. Если имеются технические средства в виде подъемника с люлькой или специальной штанги для выполнения съемки с вертикального базиса, то можно организовать фотосъемку фасада в виде двух перекрывающихся и параллельных маршрута (рис. 7а, 8). Для этого необходимо рассчитать поперечный (вертикальный) базис фотографирования BV. Он вычисляется по тем же формулам, что и горизонтальный базис. Предположим, что нам необходимо рассчитать такой базис, чтобы он обеспечивал 30% перекрытия между маршрутами, тогда:
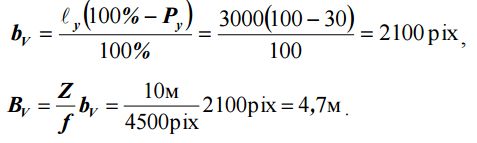
На рис. 7, а показана схема фотосъемки для данного случая, а на рис. 11 – расположение вертикального базиса относительно объекта. В данном случае уже требуется 16 снимков.
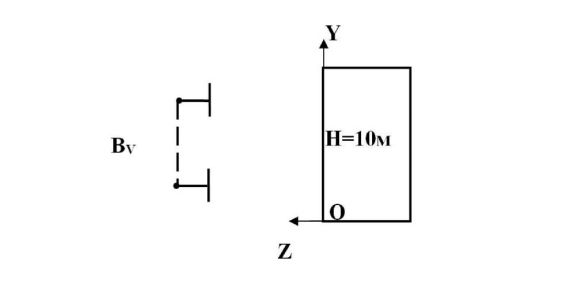
Рис. 11. Схема проектирования фотосъемки высокого объекта. Вариант с вертикальным базисом.
Второй вариант. Если невозможно организовать вертикальный базис фотографирования, то выполняют наклонную фотосъемку под разными углами с тем, чтобы обеспечить фотосъемку верхней части здания (рис. 7б). В этом случае вычисляют наклонное расстояние от точки фотографирования до верхней кромки здания, которое будет естественно больше, использованного нами отстояния для расчета базиса фотографирования, а, следовательно, в этой части здания точность определения координат точек объекта будет ниже заданной.
Поэтому, для наклонной съемки следует рассчитать новое значение базиса фотографирования. В нашем случае наклонное отстояние Z' (рис. 12) будет:
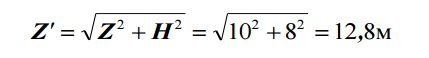
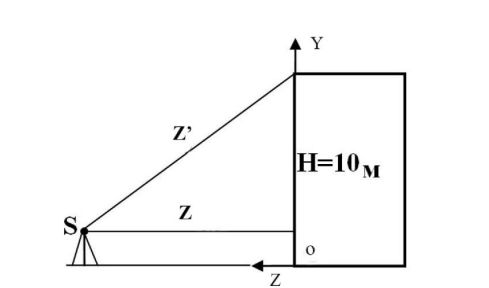
Рис. 12 Схема проектирования фотосъемки высокого объекта. Вариант наклонной съемки.
Здесь в качестве высоты здания H взято 8 м из предположения, что камера (точка S) в момент съемки будет находиться примерно на высоте 2 м.
Значение базиса фотографирования для наклонной съемки равно:
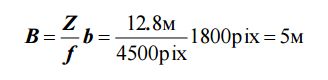
при этом
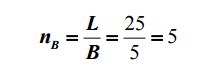
Итак, схема фотосъемки в этом случае может выглядеть следующим образом (рис. 7б) (наклонные снимки показаны пунктиром). Всего получается 14 снимков.
Третий вариант. Рассчитаем параметры фотосъемки, если камеру повернуть на 90°, т.е. сориентировать длинную сторону кадра по вертикали (рис. 13). Тогда:
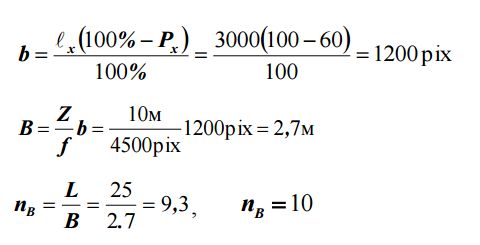
при этом захват по вертикали равен
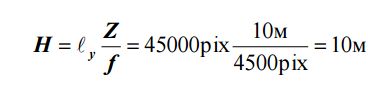
т.е. высоте самого здания. В этом случае достаточно сделать один маршрут из 11 снимков и покрыть фотосъемкой все здание, как на рис. 13.
Таким образом, любой из трех вариантов может быть осуществлен на практике и обеспечит заданную точность определения координат точек объекта. Однако из этих трех вариантов оптимальным можно считать третий, т.к. он наиболее просто реализуется и имеет меньшее количество снимков.
При фотосъемке сложных по форме архитектурных сооружений могут возникнуть мертвые зоны, что требует дополнительного проектирования фотосъемки этих зон. На рис. 2.13 показан пример мертвой зоны и схемы ее фотосъемки.
Для создания обмерных чертежей немаловажным является возможность дешифрирования мелких объектов. Это зависит от размера ∆ одного пикселя изображения в масштабе объекта. Вычислим ∆, разделив величину захвата H, полученную для конкретного отстояния Z, на соответствующее количество пикселей в кадре ℓy:
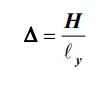
В нашем случае, при отстоянии Z = 36 м, H = 24 м и ℓy = 3000 pix, размер пикселя на объекте будет ∆ = 0,008 м, а при отстоянии Z = 10 м, H = 6,7 м и ℓy = 3000 pix, ∆ = 0,002 м.
Если такое разрешение не удовлетворяет поставленной задаче, то в этом случае следует уменьшить отстояние с тем, чтобы получить требуемый размер пикселя на объекте, а затем естественно следует пересчитать значение базиса фотографирования и сделать новый проект фотосъемки.
Предрасчет точности определения координат точек объекта по стереопаре снимков позволяет установить требования к точности определения координат и высот опорных точек, определяемых геодезическими методами. Средние квадратические погрешности определения координат и высот опорных точек должны быть не более 1/3 от значений средних квадратических погрешностей определения координат и высот точек объекта по стереопаре снимков.
#стереофотограмметрическаясъемка #фотограмметрия #наземнаясъемка #расчет #съемка #обмерныерботы #архитектурнаяфотограмметрия
















 Программный комплекс ScanIMAGER предназначен для обработки результатов трехмерного лазерного сканирования применительно к архитектурным обмерам. Он построен по модульному принципу и поставляется в различных модификациях.
Программный комплекс ScanIMAGER предназначен для обработки результатов трехмерного лазерного сканирования применительно к архитектурным обмерам. Он построен по модульному принципу и поставляется в различных модификациях.